Le Département d’Astrophysique (DAp) du CEA est fortement impliqué dans le développement...
Lire la suite


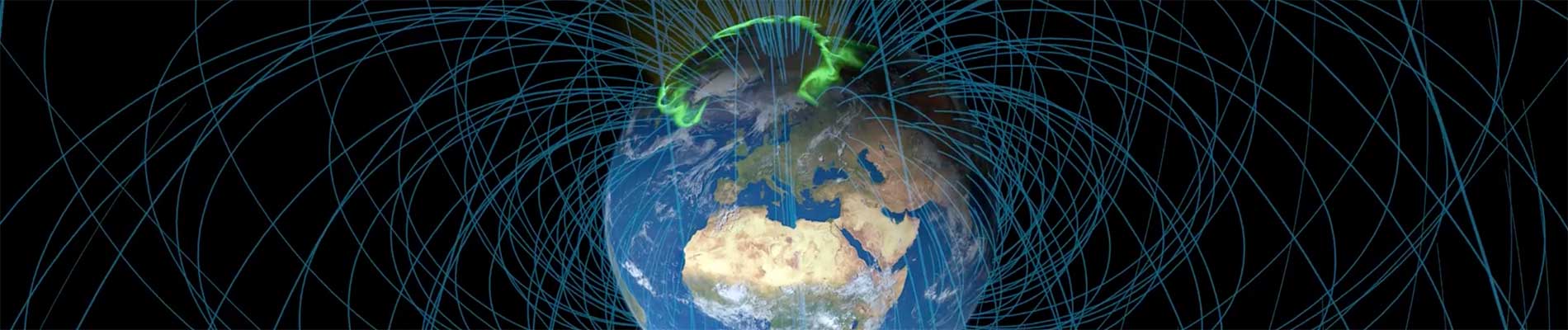
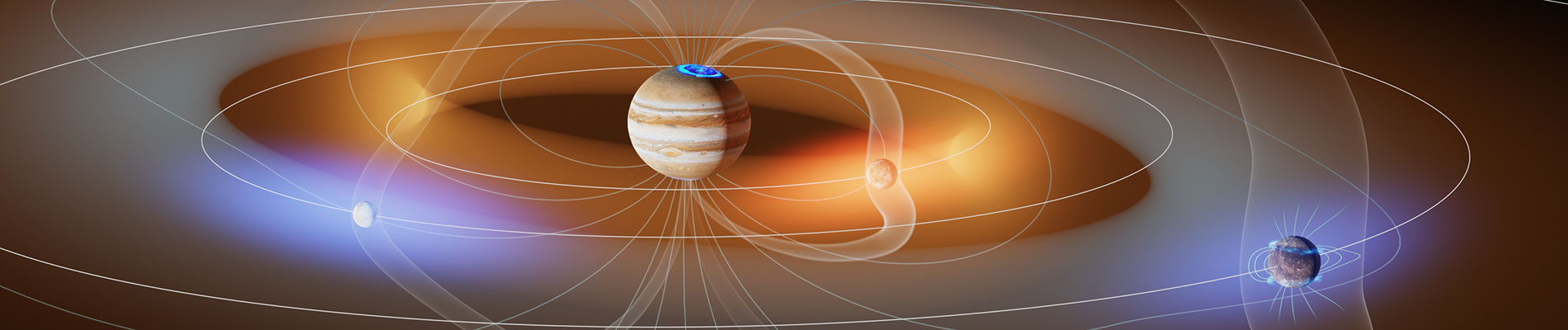






Action Thématique Soleil-Terre (ATST)
L’Action Thématique Soleil-Terre (ATST¹) est une composante du Programme National Astrophysique (PN Astro) du CNRS Terre et Univers (INSU). L’ATST a pour objectif de financer des projets de recherche et d’animer la communauté scientifique nationale autour de la physique des plasmas héliosphériques. Les grandes thématiques de l’ATST sont :
- Le Soleil magnétique – son intérieur et son atmosphère – son activité, ses éruptions ;
- Le vent solaire – depuis le Soleil jusque dans le milieu interplanétaire – son origine, son accélération, ses perturbations ;
- Les magnétosphères et ionosphères – de la Terre, des planètes du système solaire, et des exoplanètes – leurs réponses aux forçages solaires, leurs événements impulsifs ;
- L’héliosphère – dans sa globalité, jusqu’à son interaction avec le milieu interstellaire – les mécanismes qui la structurent ;
- La météorologie de l’espace – la prévision des perturbations solaires géoeffectives, la surveillance du Soleil, de l’environnement spatial et des impacts sur les enveloppes de la Terre et des autres planètes.
Une spécificité de la communauté ATST est l’étude des processus physiques de base qui existent dans des conditions physiques très variées, telles qu’on peut les trouver dans les plasmas héliosphériques. Il s’agit notamment de comprendre :
- Comment fonctionnent la dynamo solaire et le processus d’émergence de flux ;
- Comment se déclenchent les instabilités et les rétroactions aux grandes échelles en régime fluide et non-collisionnel ;
- Quels sont les effets de physique atomique sur l’ionisation, le transfert radiatif, et la polarisation de la lumière ;
- Quels sont les mécanismes d’accélération du plasma et des particules énergétiques et de la dissipation par les chocs, la reconnexion magnétique, les ondes et la turbulence ;
- Comment porter des résultats de recherche fondamentale vers des outils appliqués pour la météorologie de l’espace.
¹ L’ATST est issue de l’ancien Programme National Soleil-Terre (PNST)
Evénements à venir
Parker 4
10th MMS Anniversary and 11th Community Workshop
French AtLAST days
In situ heliospheric science meeting
L'Aquila International school 12-16 May 2025 on Cross-scale coupling of Heliophysics Systems
Atelier communautaire M-MATISSE - 19-23 mai 2025 Londres
Nos dernières Annonces
2 Postdoc Positions at the University of Bern in solar and stellar
The Space Weather group within the Astronomical Institute at the University of...
Lire la suiteProfessorship in Astrophysics at the Dublin Institute for Advanced Studies
The Astronomy & Astrophysics Section at the Dublin Institute for Advanced Studies...
Lire la suiteEditor in Chief search : « Space Weather » – AGU/Wiley
« Space Weather » (AGU/Wiley) publishes research and commentary on understanding and predicting space...
Lire la suiteBepiColombo Call for Interdisciplinary Scientist and Guest Investigators — advance notice
BepiColombo is a joint mission by ESA and JAXA to study Mercury,...
Lire la suiteIRIS Call for Science Planners AO#11 — advance notice
NASA’s Interface Region Imaging Spectrograph (IRIS) is a Small Explorer (SMEX) mission...
Lire la suitePoste permanent en physique stellaire dans le contexte de la mission PLATO
Le Département d’Astrophysique (DAp) du CEA est fortement impliqué dans...
Lire la suite2 Postdoc Positions at the University of Bern in solar and stellar flare research
The Space Weather group within the Astronomical Institute at the...
Lire la suiteProfessorship in Astrophysics at the Dublin Institute for Advanced Studies
The Astronomy & Astrophysics Section at the Dublin Institute for...
Lire la suiteEditor in Chief search : « Space Weather » – AGU/Wiley
« Space Weather » (AGU/Wiley) publishes research and commentary on understanding and...
Lire la suiteBepiColombo Call for Interdisciplinary Scientist and Guest Investigators — advance notice
BepiColombo is a joint mission by ESA and JAXA to...
Lire la suiteIRIS Call for Science Planners AO#11 — advance notice
NASA’s Interface Region Imaging Spectrograph (IRIS) is a Small Explorer...
Lire la suite